近年、企業や組織がデータ活用に注力する中、適切なデータ分析手法の理解が重要視されています。その中でも「ロジスティック回帰分析」は、マーケティングをはじめとする幅広い分野で用いられており、データ分析をする上で理解しておくべき手法と言えます。
そこで今回は、ロジスティック回帰分析の概要や活用例、Excelを使った計算方法、分析を行う際の注意点について解説します。
この記事を通じて、ロジスティック回帰分析の基本的な考え方や分析方法などを習得できるので、データ分析のスキルアップを目指す方は、ぜひ参考にしてみてください。
ロジスティック回帰分析とは?【確率を分析する手法】
ロジスティック回帰分析は、2つの値のデータ(例:成功・失敗)に使われる分析手法です。主に事象の発生確率を予測するために用いられます。ここからは、ロジスティック回帰分析について詳しく解説します。
オッズとオッズ比で影響度を判断する
ロジスティック回帰分析では、各要因の影響度をオッズ(確率を表す数値)とオッズ比(2つのオッズの比較を表す数値)で判断します。ロジスティック回帰分析を使うことで、特定の事象が発生する確率を求められ、その事象が発生する要因を説明しやすくなります。
例えば、「勉強時間」「睡眠時間」「経歴」といった複数のデータを集め、特定の企業への就職率を求めた場合、どういった「勉強時間」「睡眠時間」「経歴」を持つ人が内定をもらいやすいかの分析を行えます。
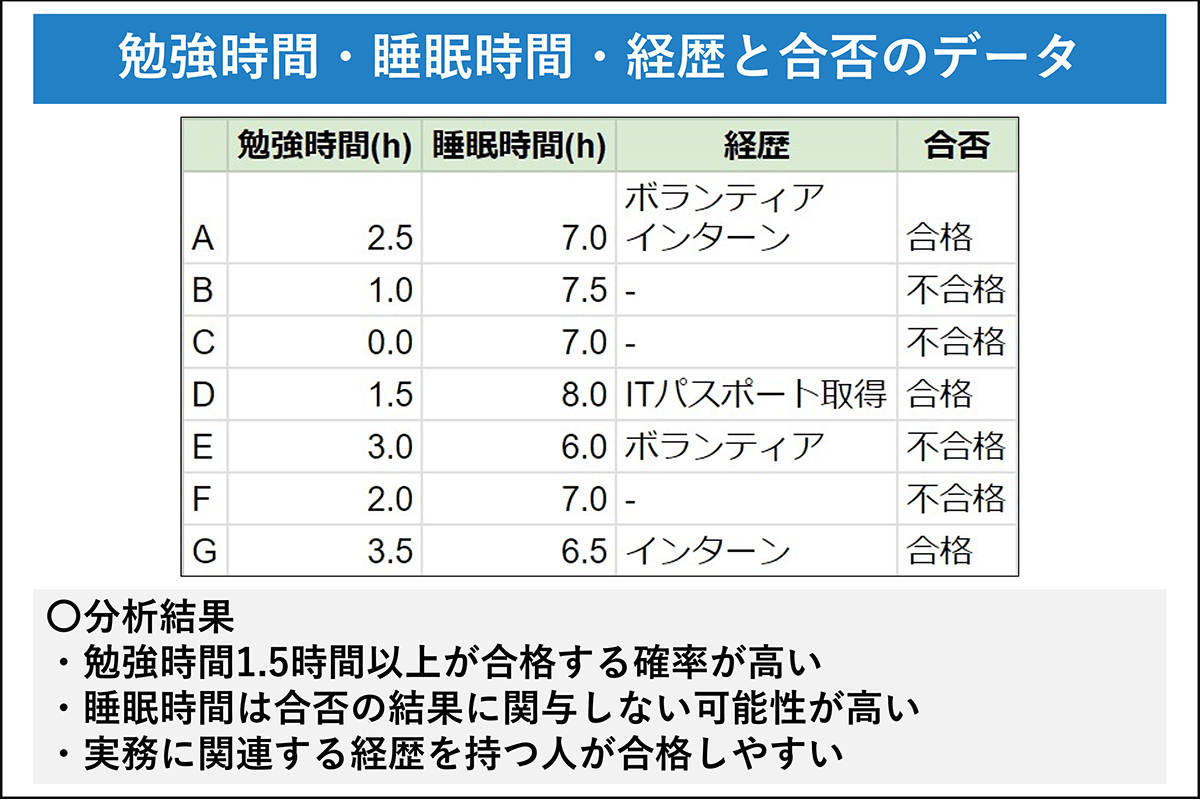
このようにロジスティック回帰分析は、集めたデータを基に成功の確率を求めた上で、何故その傾向にあるのかを導き出せる分析です。
重回帰分析との違いは「質」か「量」か
ロジスティック回帰分析と重回帰分析は、どちらも統計学で使われる分析手法です。重回帰分析は、個数などの量的データを予測するのに用いられます。
一方、ロジスティック回帰分析は、ある事象が起こる確率を予測する質的な分析手法です。
例えばマーケティングの場面では、重回帰分析で購入者数を予測し、ロジスティック回帰分析では個々の顧客の購入確率を算出します。
このように、ロジスティック回帰分析と重回帰分析との違いは「質」と「量」にあります。
ロジスティック回帰分析の活用例
ロジスティック回帰分析は、さまざまな分野で活用されている分析手法です。例えば、マーケティング分野では、顧客の購買行動の予測などに用いられます。
また、気象予測にもロジスティック回帰分析は活用されています。さらに、不正の検知や病気の発症予測にも活用されることが多いです。以下では、ロジスティック回帰分析の活用例について解説します。
マーケティング
ロジスティック回帰分析は、マーケティング分野で活躍しています。具体的な活用例としては、顧客の商品購入確率の予測にロジスティック回帰分析が用いられます。
この際に使用されるデータは、顧客の購買履歴や行動データなどです。また、性別や年齢などの属性と購入商品の関係性の分析やキャンペーンの効果測定、購入時の流入経路の分析にも活用されています。
特定の商品を購入する際に、どのページを閲覧していたか、どこに注目していたか、性別・年齢により異なる行動パターンを導き出すことで、流入した人にあわせたページ作りができます。
気象予測
ロジスティック回帰分析は気象学の分野でも活用され、過去の気象データから気温、天気などの予測に用いられます。さらに、気象予測はイベントの日程選定や販売数量の調整にも役立つため、マーケティングの観点からも注目されています。
不正の検知
ロジスティック回帰分析は、サーバーやシステムへの不正アクセス検知にも活用可能です。不正の有無とデータの関係を解析することで、数値の異常からシステムへの不正侵入を特定できます。
さらに、不正ユーザーの行動パターンを分析し、予測モデルを構築することで、早期の不正検知と防止策の実施が可能となります。ロジスティック回帰分析は、サイバーセキュリティの強化に欠かせない手法といえるでしょう。
病気の発症予測
病気の発症予測にも、ロジスティック回帰分析は活用されています。この手法では、患者の症状や生活習慣などのデータを基に、病気の有無や発症を予測することが可能です。
さらに、発症していない場合でも、その確率を算出することで、病気の予防と生活習慣の改善に役立てられます。ロジスティック回帰分析は、医療分野におけるデータ活用の一例であり、患者の健康管理に貢献しています。
Excelを使ったロジスティック回帰分析の計算方法
Excelには、回帰分析や分散分析のための関数や「分析ツール」が用意されています。しかし、ロジスティック回帰分析の機能は含まれていません。
しかし、ロジスティック回帰分析の基本原理を理解していれば、ソルバー(最適解を表示するExcelの機能)を使用してロジスティック回帰分析を実行することが可能です。以下では、Excelを使ったロジスティック回帰分析の計算方法について解説します。
データを整理する
ロジスティック回帰分析を開始する前に、使用するデータをまとめて、表を作成しましょう。ここで準備するデータが傾向の分析に関わってきます。
なお、本解説で用いるのは、架空の企業における社員のテスト結果を予測するために作成されたダミーデータです。説明変数として、社員研修の参加有無(0:不参加、1:参加)とテスト勉強時間を設定しました。目的変数であるテスト結果は、0が不合格、1が合格を表すダミー変数です。
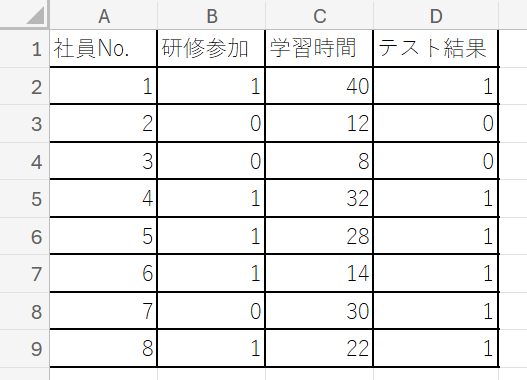
① 最初に、新規でシートを作ります。次に、元のデータシートの「D1:D9」の範囲をコピーし、新しいシートの「A3:A11」にペーストしてください。

② 次に、元データの「B1:C9」をコピーし、新規シートの「C3:D11」の範囲に貼り付けます。
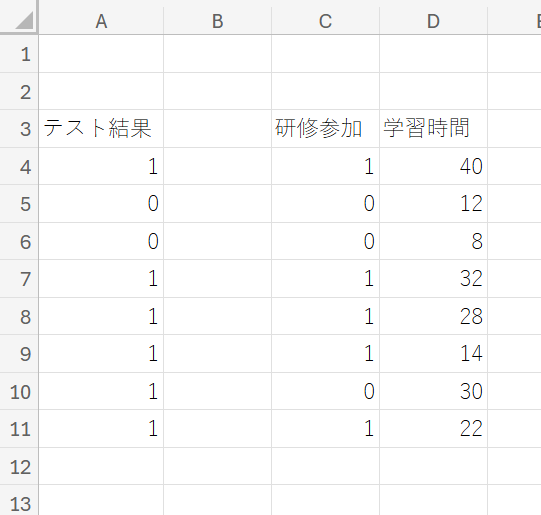
③ セル「B3」に「定数項」と入力後、「B4:B29」の範囲のセルすべてに「1」を入力してください。
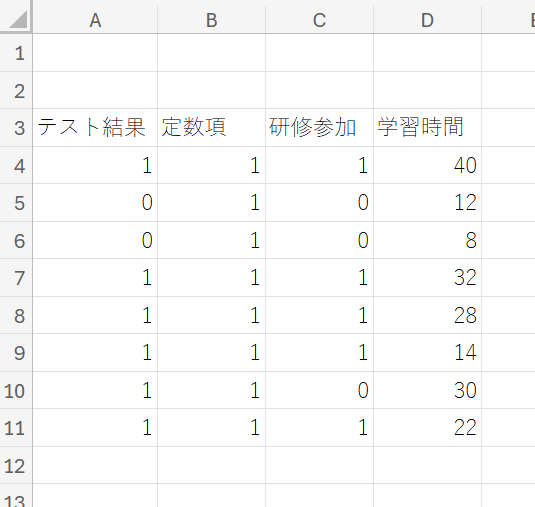
A列の「テスト結果」は目的変数、B列からD列の「定数項」「研修参加」「学習時間」は説明変数となります。
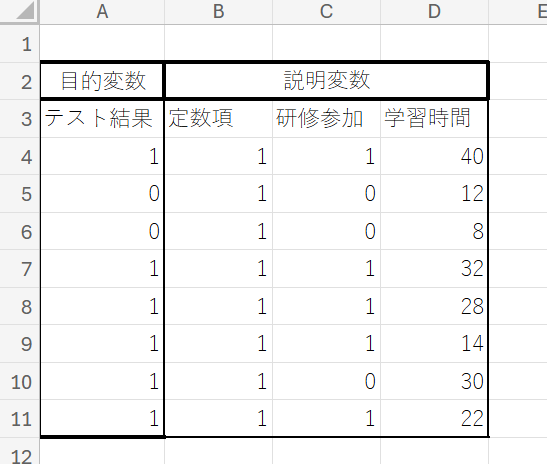
④ セル「B1:D1」の範囲に、「0」を入力してください。
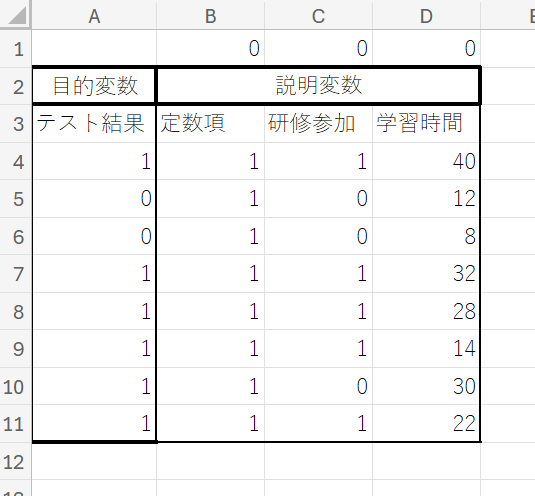
⑤「B1:D1」のセルは「偏回帰係数の推定値」を表し、ソルバーを使ってこの値を変化させることで解を導きます。ここでは、すべての偏回帰係数の初期値を「0」に設定しています。
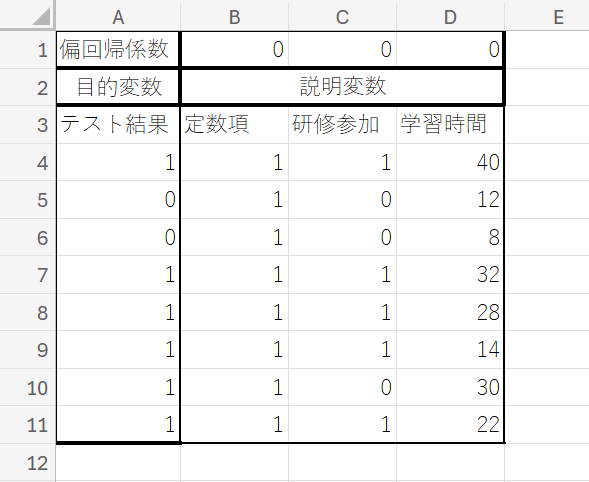
推定値・対数尤度(たいすうゆうど)を設定する
次に、推定値・対数尤度(たいすうゆうど)を設定します。推定値は、説明変数が目的変数に及ぼす影響の大きさを数値化したものです。
また対数尤度は、現在のモデルが観測データにどの程度適合しているかを示す指標を表します。以下では、推定値・対数尤度を設定する手順を紹介します。
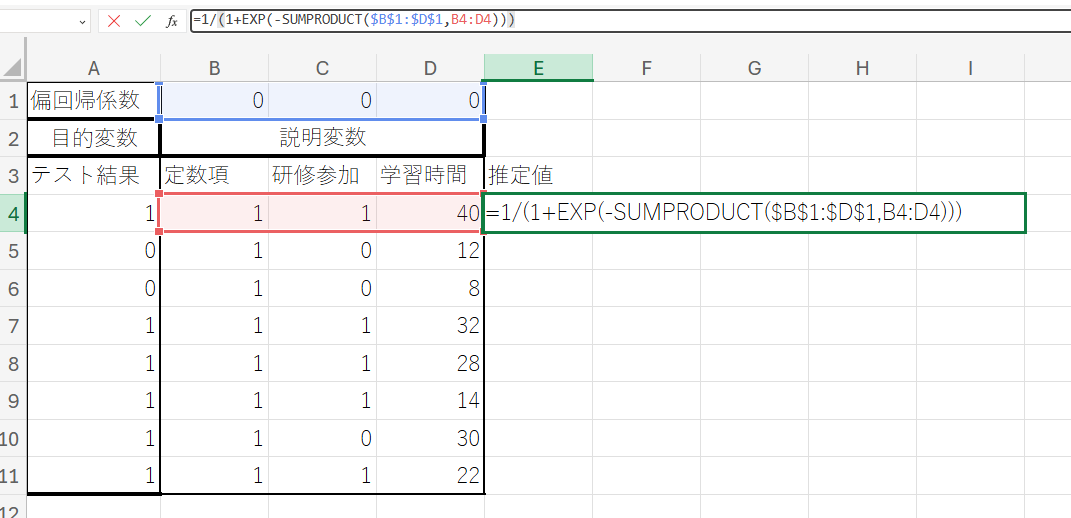
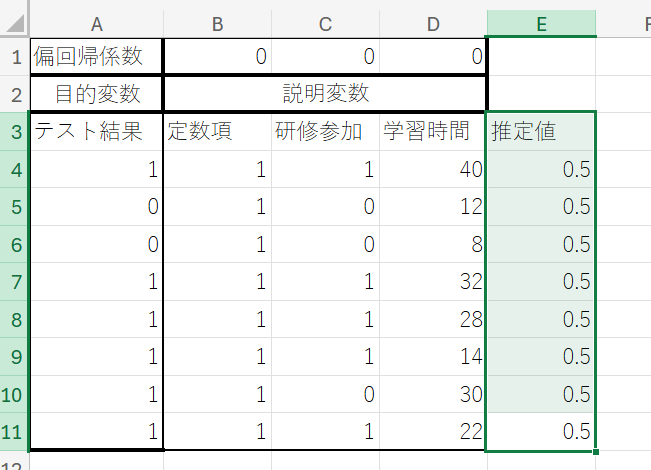
① セル「E3」に「推定値」と入力した後、セル「E4」に以下の数式を入力し、Enterキーを押します。
『 =1/(1+EXP(-SUMPRODUCT($B$1:$D$1,B4:D4))) 』
この数式は、各データ点においてy=1となる確率の推定値『 p^ (y=1∣x) 』を算出するものです。ここで用いられているEXP関数は指数関数の計算に、SUMPRODUCT関数は引数として与えられた配列の積和を求めるのに使用されます。この数式を入力することで、モデルの予測値が計算されます。
② セル「E4」の右下角にカーソルを合わせ、形状が+に変化したらダブルクリックしてください。この操作により、「E5:E11」のセルまで数式がオートフィルされます。
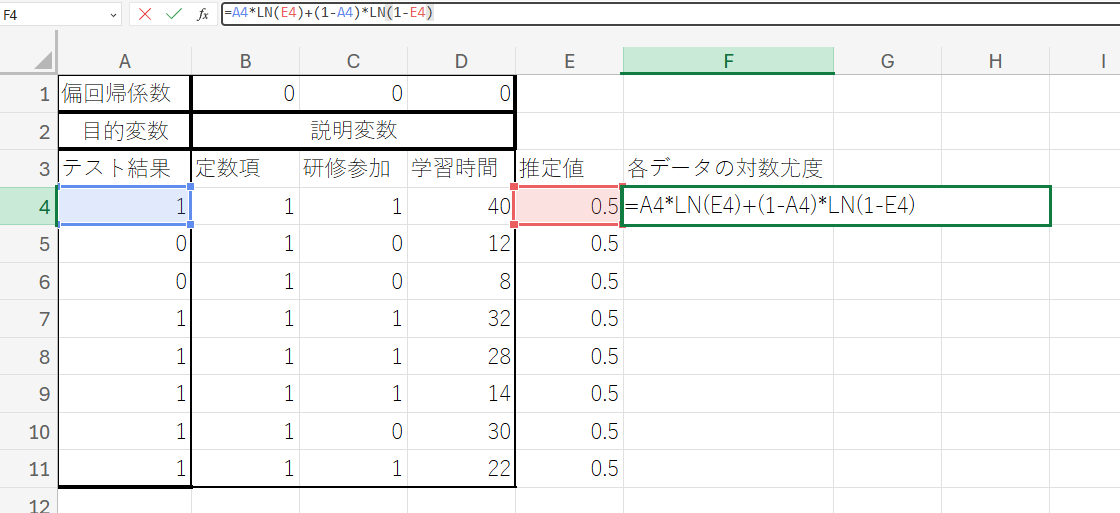
③ セル「F3」に「各データの対数尤度」と入力後、セル「F4」に以下の数式を入力し、Enterキーを押してください。
『 =A4*LN(E4)+(1-A4)*LN(1-E4) 』
この数式は、各観測データの対数尤度を計算するものです。ここで用いられているLN関数は、引数の自然対数を求める関数です。この数式により、個々のデータの対数尤度が算出されます。
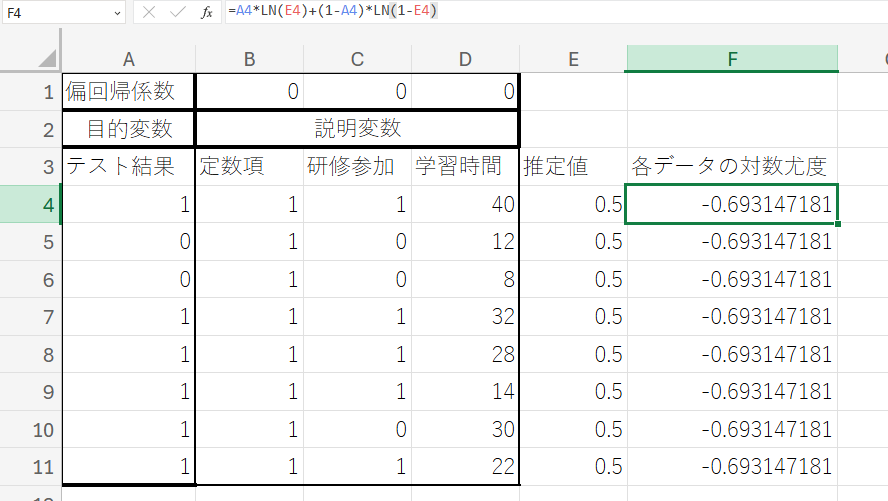
④ セル「F4」の右下角にカーソルを合わせ、形状が+に変化したらダブルクリックします。これにより、「F5:F11」のセルまで数式がオートフィルされます。
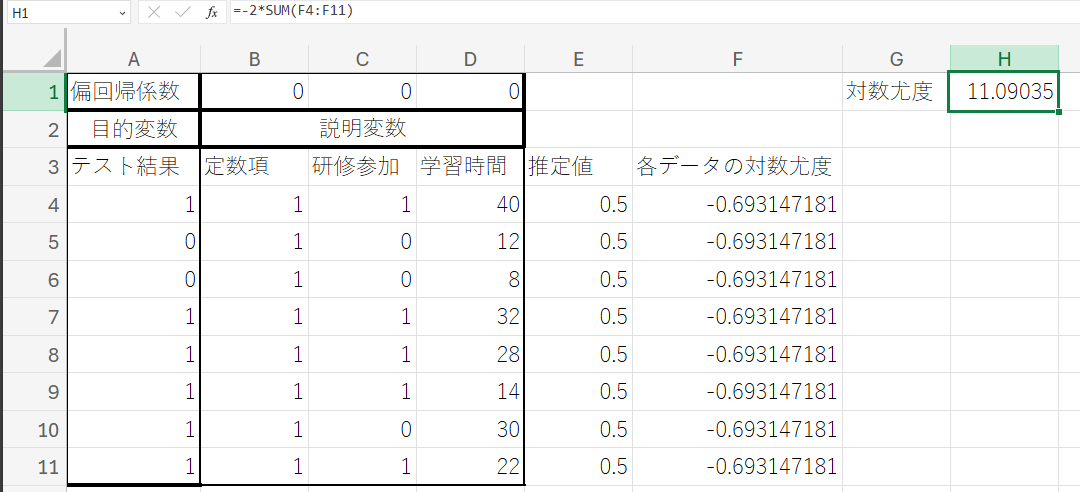
⑤ セル「G1」に「対数尤度」と入力した後、セル「H1」に以下の数式を入力し、エンターキーを押してください。
『 =-2*SUM(F4:F11) 』
この数式は、モデル全体の対数尤度の総和にマイナス2を乗じた値を計算します。ここで用いられているSUM関数は、指定された範囲の和を求める関数です。
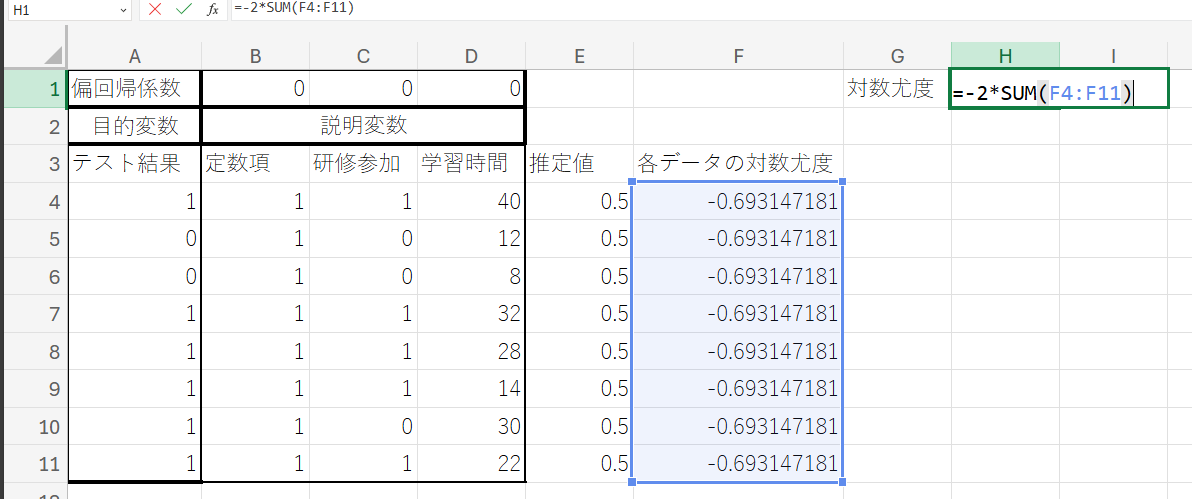
入力後のシートは以下のようになります。
ソルバーを設定する
次に、ソルバーを使用して偏回帰係数の推定を実施します。まず、ソルバーを有効化するために以下の手順を実行してください。
① ソルバーの有効化(有効化されている場合は、2に移ってください)
a) Excelの[ファイル]タブをクリックし、表示されたメニューから[オプション]を選択します。
b)「Excelのオプション」ウィンドウが開いたら、[アドイン]をクリックしてください。
c)「管理」のドロップダウンリストから[Excelアドイン]を選び、「設定」をクリックします。
d)「アドインの選択」ウィンドウで「ソルバー アドイン」のチェックボックスにチェックを入れ、「OK」をクリックしてください。
以上の手順により、ソルバーが有効化され、偏回帰係数の推定が可能になります。
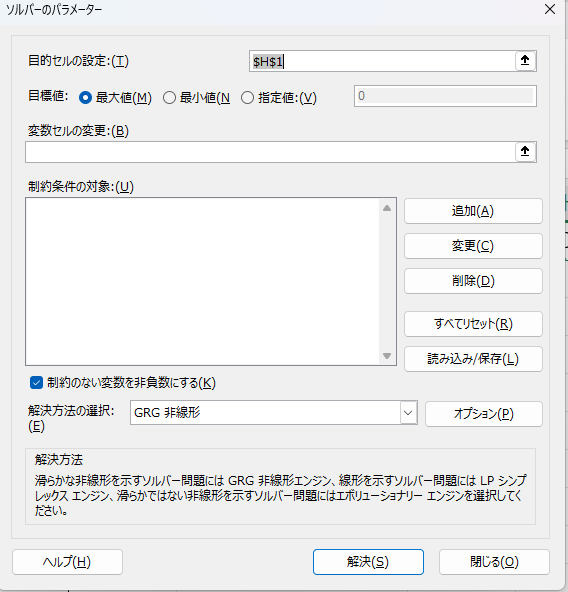
② セル「H1」を選んだ状態で、「データ」タブから「ソルバー」をクリックしてください。ソルバーのウィンドウが開きます。
「目的セルの設定」に「$H$1」と入力されていることを確認します。
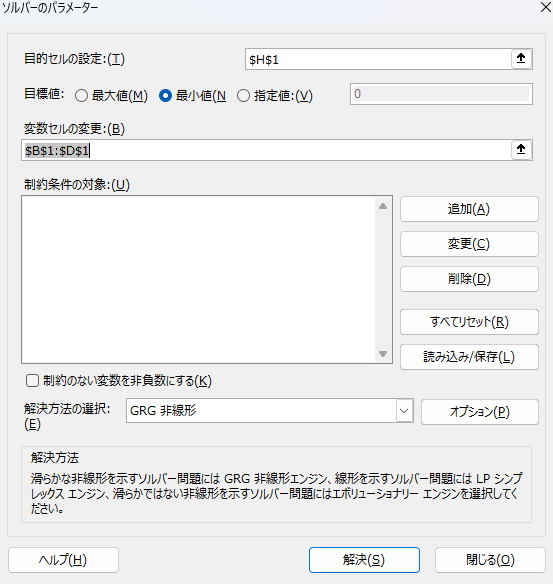
③ ソルバーのウィンドウでは、「目標値」の設定で「最小値」を選択し、「変数セルの変更」には「$B$1:$D$1」と入力してください。「制約のない変数を非負数にする」にチェックが入っている場合は、チェックを外します。これらの設定が完了すると、ソルバーのウィンドウは以下のようになります。
計算を実行しモデルを求める
① 次に、「解決」をクリックします。ソルバーは「B1:D1」の3つの偏回帰係数の値を調整しながら、セル「H1」に入力された対数尤度のマイナス2倍を最小化します。これにより、偏回帰係数の最適値が求められます。
また、対数尤度を変化させて解を導出するこの方法は「最尤法」と呼ばれています。計算が終了すると、結果を示す以下のウィンドウが表示されます。
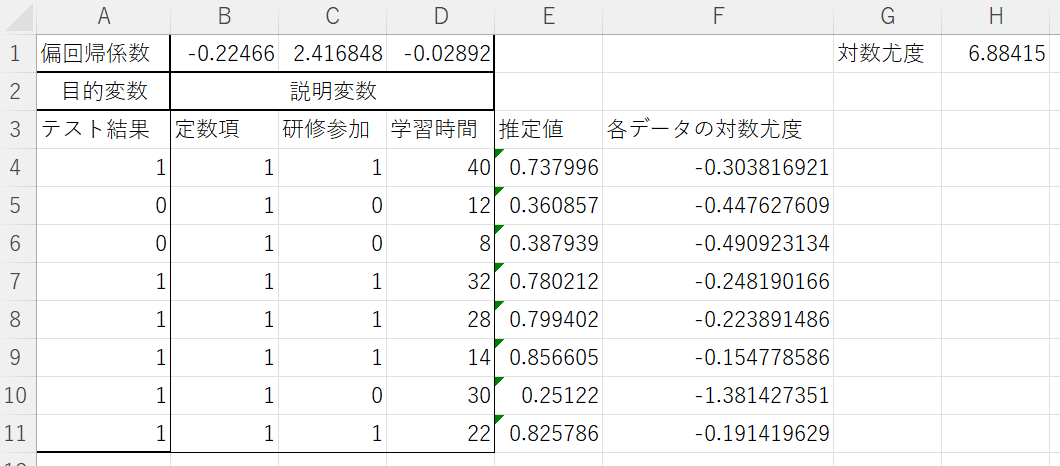
② 偏回帰係数のセル「B1:D1」の値を確認すると、変化が見られます。
この結果より、導き出されたロジスティックモデルは以下の式で表現されます。
『 Ln(p/1-p)= -0.22+2.41×研修参加+(-0.028×学習時間) 』
③ 推定値の部分も確認すると、「y=1となる確率」が表示されています。「試験結果=1」に近いデータは、「試験結果=0」に近いデータと比べて、確率が高くなっていることがわかります。
ロジスティック回帰分析を行う際の注意点
ロジスティック回帰分析を行う際には、いくつかの注意点があります。第一に、分析対象のデータは0と1を用いなければなりません。
さらに、高精度な結果を得るためには、十分な量のデータが必要です。以下では、ロジスティック回帰分析を行う際の注意点を解説します。
0と1で表せるデータを用いる必要がある
ロジスティック回帰分析では、説明変数と目的変数が0か1で表現できるデータを用いる必要があります。これは、従属変数が連続値の線形回帰とは異なる特徴です。
データが0と1の有無で表せない場合、「多項ロジスティック回帰」や「序数ロジスティック回帰」といった手法を適用しなければならず、分析がより複雑になります。
高い精度を得るにはデータ数が大きい必要がある
ロジスティック回帰分析で高精度な結果を得るには、十分な数のデータが欠かせません。データ数が少ない場合、外れ値の影響を過度に受けてしまい、正確な分析が困難になることがあります。
複数の要因を考慮した分析を行うためにも、ある程度データが集まってから分析を実施するのがいいでしょう。
まとめ
今回の記事では、ロジスティック回帰分析の概要や活用例、Excelを使ったロジスティック回帰分析の計算方法、分析を行う際の注意点などについて解説しました。ロジスティック回帰分析は、ある事象の発生確率を予測する手法であり、オッズとオッズ比で各要因の影響度を判断します。
質的なデータを扱う点で重回帰分析と異なり、マーケティングや気象予測、不正検知、病気の発症予測など、幅広い分野で活用されています。ただし、分析には0と1で表現できるデータを用い、高精度な結果を得るには、十分なデータ数が必要であることに注意しましょう。


